Computer Science is Easy

Simplifying Computer Science for everybody

Two’s complement: how to store negative integers in binary

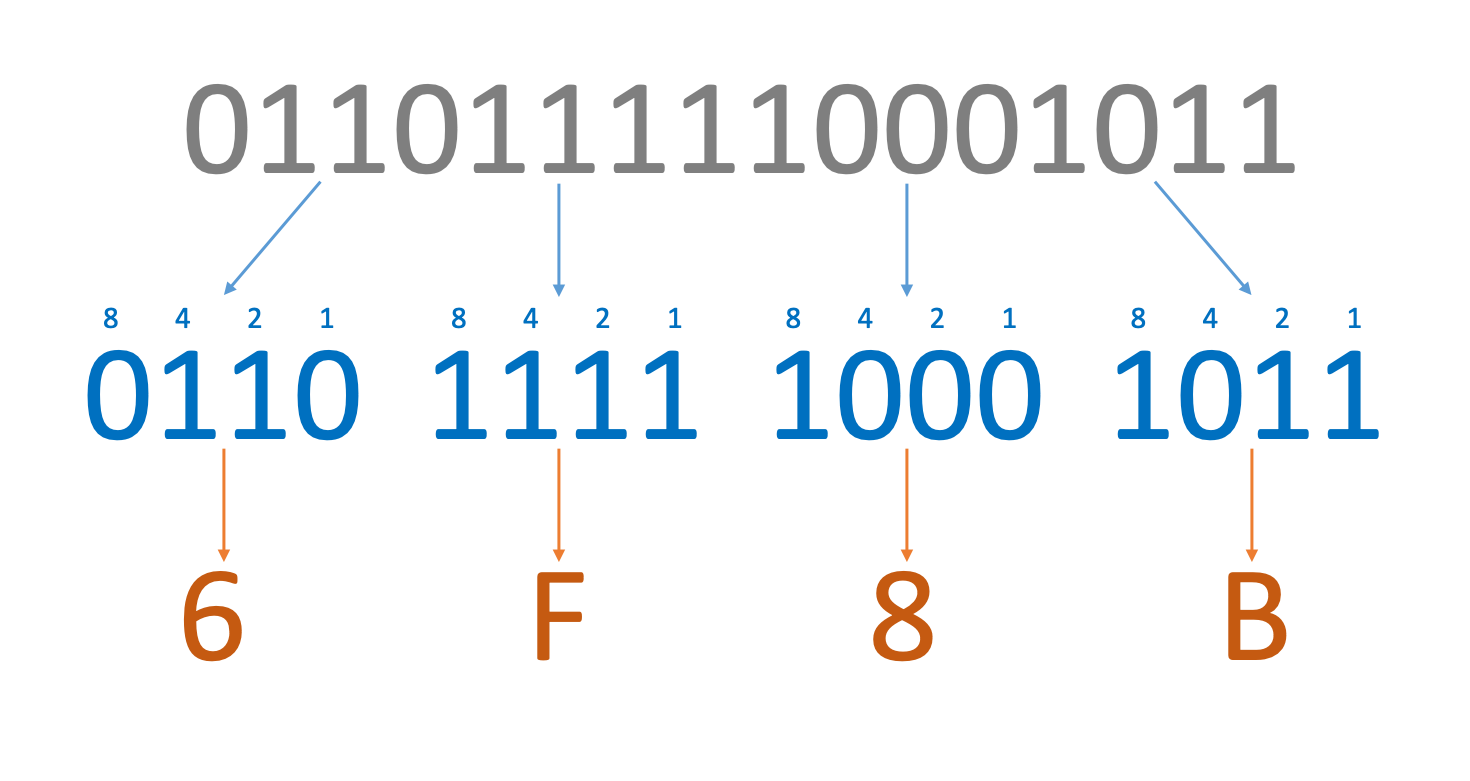
Up to this point, we have only dealt with how to encode positive integers in binary. To encode negative integer values you must use two’s complement binary encoding. You are used to using eight bits to store any of 256 possible values ranging from 0 to 255. In two’s complement, you still use eight bits to store any of 256 possible values, but this time they range from -128 to 127. Two’s complement is an encoding method that is, at first, a little confusing. However, once you understand the process it is actually very simple. There are two methods. Both methods involve working with a value and flipping the sign (e.g. if you want the two’s complement binary for -56, write out the binary for 56 and then perform the calculations required to flip the sign, giving you -56). Note that the same method can be also used to convert a negative value into a positive one. In our examples below, we will convert 116 into -116 using two’s complement encoding.

Method 1

This method is simple. Firstly, write out the binary value:

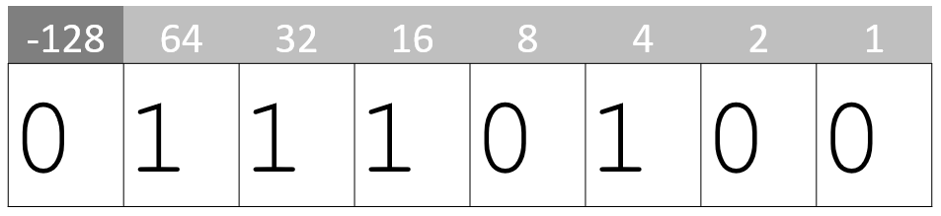
Note that the Most Significant Bit (MSB) is used to represent -128, not 128. You can use this to check your answers if you’re unsure in the exam.

Next, flip every bit:

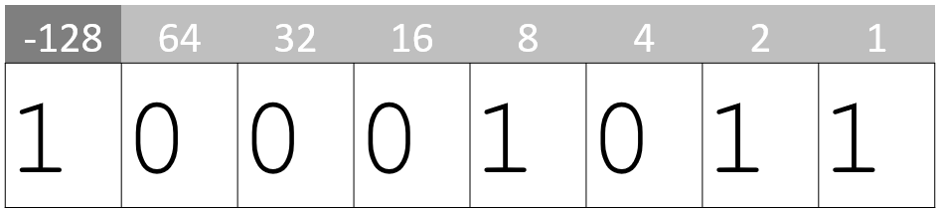
Finally, using binary addition[1], add 1 to the value:

You now have the two’s complement binary encoding for -116.

Method 2

Start from the Least Significant Bit (LSB), moving left until you find a 1:

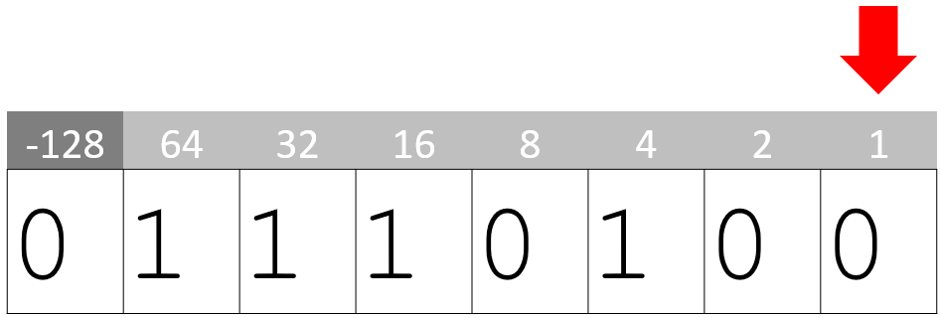
 Ignore the first ‘1’:

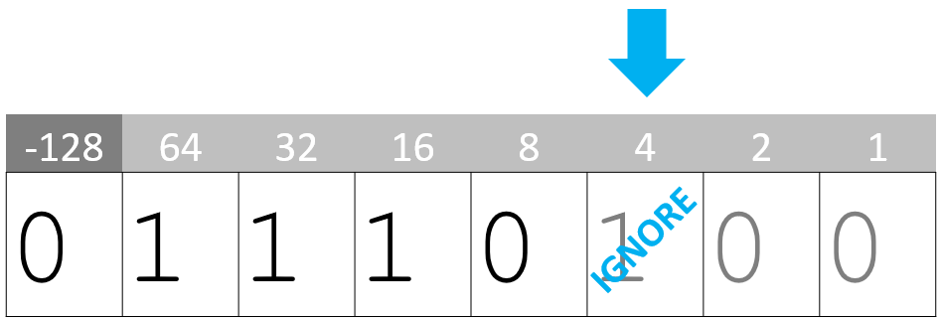
Flip every bit that follows:

You now have your answer.

A few important notes

Firstly, two’s complement is used to encode positive values as well as negative values. If you’re asked to give the two’s complement for a positive value, it’s exactly the same as it would be if it were encoded as a standard binary integer. Read the question carefully.

Two’s complement values don’t have the same range as their positive binary integer equivalents. You can’t store 128 in an 8-bit two’s complement value. You’ll need at least nine bits to store it. Be careful.

All two’s complement values where the MSB is ‘1’, are negative. Always. The opposite is also true.

Finally, if you ever need to pad bits (i.e. add more bits to the left of a binary value to make it a certain length, such as a byte), just as you’d use zeroes to pad a positive value (e.g. 0011 -> 00000011), you must use ones to pad a negative value (e.g. 1011 -> 11111011).

[1] Put simply, binary addition is very similar to denary addition, including ‘carrying the one’. The only difference is that digits can only range from 0-1. Binary addition depends on some very simple rules: 0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 0 carry 1; 1 + 1 with a carried 1 = 1 carry 1. You can find plenty of online tutorials for this if you wish to understand it further.

Memory and file size units in binary

As you most likely know already, a single digit in binary is called a bit (short for binary digit). An eight-bit value is called a byte. A four-bit value, which is half a byte, is called a nibble.

There are also several units that we use to represent larger numbers of bits. You will probably be most familiar with these:

NameNumber of bytesEquivalent value
1 kilobyte (1 KB)1 0001000 bytes
1 megabyte (1 MB)1 000 0001000 kilobytes
1 gigabyte (1 GB)1 000 000 0001000 megabytes
1 terabyte (1 TB)1 000 000 000 0001000 gigabytes
1 petabyte (1 PB)1 000 000 000 000 0001000 terabytes


The units above are used for the sake of simplicity, as it is easy to perform the multiplication and division required to convert between the units. However, computers rely entirely on binary for their calculations, and it often makes more sense to use units that are based on this number system. You should familiarise yourself with the units below, as these are more widely used in the field of Computer Science[1].

NameExponent Number of bytesEquivalent value
1 kibibyte (1 KiB)2101 0241024 bytes
1 mebibyte (1 MiB)2201 048 5761024 kibibytes
1 gibibyte (1 GiB)2301 073 741 8241024 mebibytes
1 tebibyte (1 TiB)2401 099 511 627 7761024 gibibytes
1 pebibyte (1 PiB)2501 125 899 906 842 6241024 tebibytes

You need to know the names and the order (e.g. 1 GiB is 1024 times larger than 1 MiB) they come in, along with the exponents for the latter table. You do not need to memorise the number of bytes.

When you work with these units, it’s important to read all questions carefully. If you use the wrong unit, your answer will be wrong. Generally, a question asking for kibibytes, mebibytes, etc. will use numbers that divide more cleanly by 1024, whereas a kilobyte-based question will use more ‘round’ numbers. Still, read the question carefully.

[1] Unfortunately, kilobyte and kibibyte are often mixed up, misunderstood, and treated as if they are the same. The general understanding is that a kilobyte can be 1024 bytes or 1000 bytes, which is incorrect but very common. The kibibyte, and its associated units, are not well known outside of the field.

How to convert binary and denary to hexadecimal

Hexadecimal uses the digits 0-9 and the letters A-F, giving sixteen possible values per digit. The values are assigned like so:

Denary0123456789101112131415
Hex0123456789ABCDEF


You must be familiar with this table to be able to understand hexadecimal questions and the number system as a whole.

  1. Split the binary value into nibbles (four-bit values).
  2. Write the numbers over every bit, treating every nibble as a separate binary value (this means you write 1, 2, 4, and 8 over the digits in every nibble, starting at the right).
  3. Convert every nibble to denary. Each nibble will give you a value between 0 and 15.
  4. Convert each denary value to its hexadecimal equivalent. Use the table above if you don’t remember the equivalent values
  5. You now have the hexadecimal equivalent of the binary.

This process is shown in the diagram below:

Other conversions are also possible using similar techniques.

Converting from hexadecimal to binary

  1. Write the denary value for each hexadecimal digit.
  2. Convert each denary value into a nibble.
  3. You now have the binary equivalent of the hexadecimal value. Make sure you don’t write any spaces between the nibbles for your final answer. 

Converting from denary to hexadecimal

  1. Convert the denary value to its binary equivalent.
  2. Follow the steps for converting binary to hexadecimal.

Converting from hexadecimal to denary

  1. Convert the hexadecimal value to its binary equivalent.
  2. Follow the steps for converting binary to denary, which can be found in this post.

How to convert between binary and denary

Converting from binary to denary, and from denary to binary, is a quick and easy process that only requires very basic mathematical knowledge and skills. There are a few ways to these conversions; the techniques below are the simplest and most reliable for most people.

Converting from binary to denary

The process is as follows:

  1. Write a small 1 above the rightmost bit.
  2. Moving from right to left, write numbers above each bit, doubling the value every time. It should look like this:

    If the binary value is more than eight digits in length, keep writing the numbers, doubling the value every time (i.e. 256, 128, 512, etc.); the exam board could ask you to work with numbers as long as 16 bits in length.
  3. Add up the numbers above every bit that’s a ‘1’ (in this case, 64 + 32 + 4 + 2 = 102). The total is the denary value.

Converting from denary to binary

The process is essentially the reverse:

  1. Write the numbers above every bit, just as you did before.
  2. Find the bit with the number value that’s less than or equal to the denary value.
  3. Write a ‘1’ in that column and subtract that value from your denary.
  4. Repeat this process until your denary is 0.
  5. Fill all the remaining bits with ‘0’s.

What is binary?

There are several different number systems, each with a different base (sometimes called the radix). The base of a number system tells us how many different possible values a single digit can take. The number system we’re most used to is denary[1], which is base 10 (because it has ten possible values per digit: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9). Binary is a base 2 number system, giving it two possible values per digit (0 and 1).

In denary, every digit has a value 10 times greater than the digit to its right:

To get the overall value, we simply multiply the value of the column by the value of the digit:

(9 x 100) + (4 x 10) + (2 x 1) = 941

Binary works using exactly the same principles, except every column is worth double the column to its right:

Every digit in binary is called a bit. To convert between binary and denary integers, we need to follow the relevant process.

[1] Another common term is decimal, which is also correct.