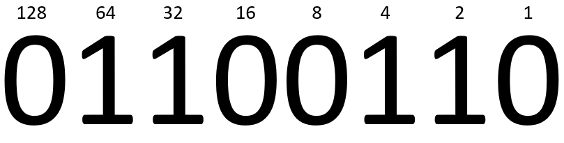Computer Science is Easy

Simplifying Computer Science for everybody

conversion

How to convert binary and denary to hexadecimal

Hexadecimal uses the digits 0-9 and the letters A-F, giving sixteen possible values per digit. The values are assigned like so:

Denary0123456789101112131415
Hex0123456789ABCDEF


You must be familiar with this table to be able to understand hexadecimal questions and the number system as a whole.

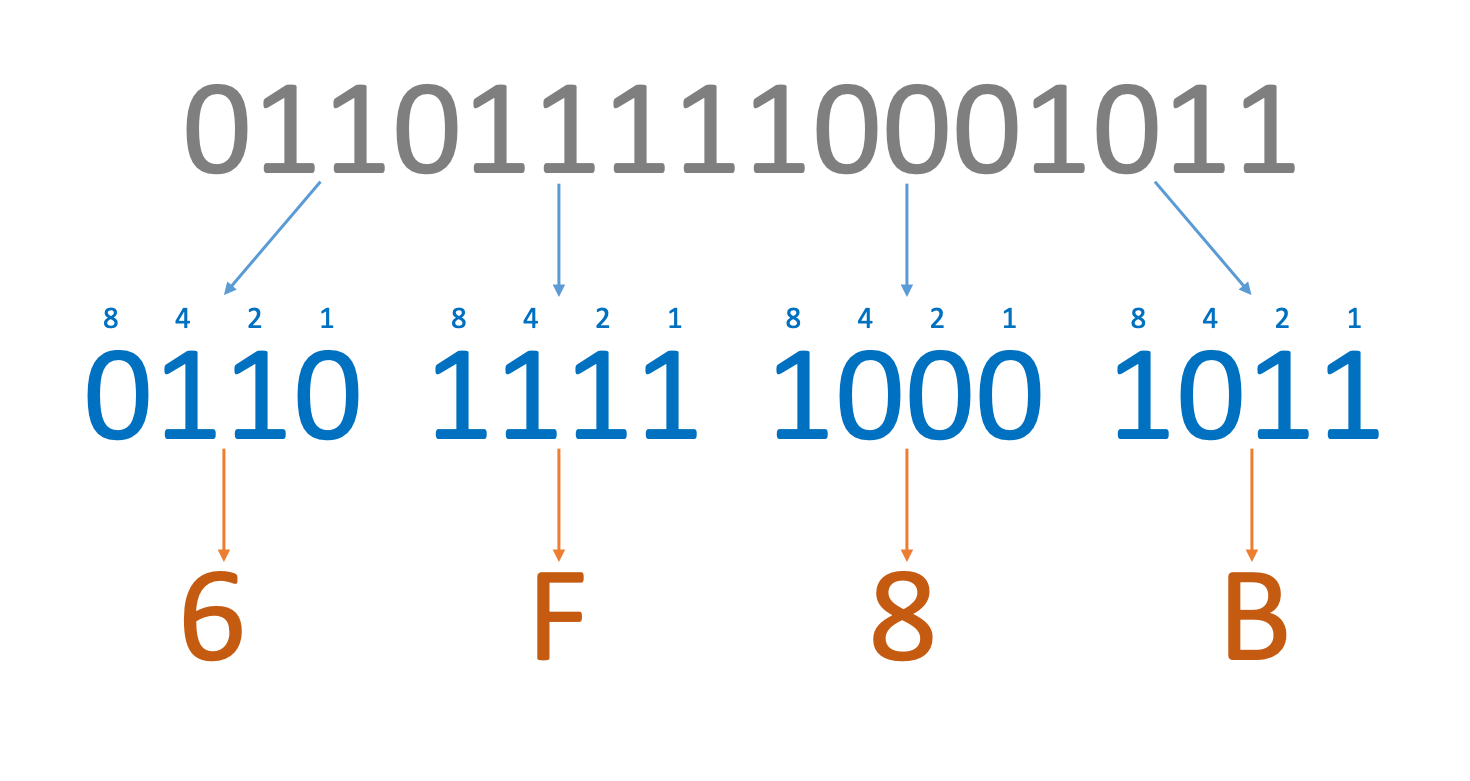
  1. Split the binary value into nibbles (four-bit values).
  2. Write the numbers over every bit, treating every nibble as a separate binary value (this means you write 1, 2, 4, and 8 over the digits in every nibble, starting at the right).
  3. Convert every nibble to denary. Each nibble will give you a value between 0 and 15.
  4. Convert each denary value to its hexadecimal equivalent. Use the table above if you don’t remember the equivalent values
  5. You now have the hexadecimal equivalent of the binary.

This process is shown in the diagram below:

Other conversions are also possible using similar techniques.

Converting from hexadecimal to binary

  1. Write the denary value for each hexadecimal digit.
  2. Convert each denary value into a nibble.
  3. You now have the binary equivalent of the hexadecimal value. Make sure you don’t write any spaces between the nibbles for your final answer. 

Converting from denary to hexadecimal

  1. Convert the denary value to its binary equivalent.
  2. Follow the steps for converting binary to hexadecimal.

Converting from hexadecimal to denary

  1. Convert the hexadecimal value to its binary equivalent.
  2. Follow the steps for converting binary to denary, which can be found in this post.

How to convert between binary and denary

Converting from binary to denary, and from denary to binary, is a quick and easy process that only requires very basic mathematical knowledge and skills. There are a few ways to these conversions; the techniques below are the simplest and most reliable for most people.

Converting from binary to denary

The process is as follows:

  1. Write a small 1 above the rightmost bit.
  2. Moving from right to left, write numbers above each bit, doubling the value every time. It should look like this:

    If the binary value is more than eight digits in length, keep writing the numbers, doubling the value every time (i.e. 256, 128, 512, etc.); the exam board could ask you to work with numbers as long as 16 bits in length.
  3. Add up the numbers above every bit that’s a ‘1’ (in this case, 64 + 32 + 4 + 2 = 102). The total is the denary value.

Converting from denary to binary

The process is essentially the reverse:

  1. Write the numbers above every bit, just as you did before.
  2. Find the bit with the number value that’s less than or equal to the denary value.
  3. Write a ‘1’ in that column and subtract that value from your denary.
  4. Repeat this process until your denary is 0.
  5. Fill all the remaining bits with ‘0’s.